Antik Çağ’ın en önemli matematikçisi, fizikçisi ve mühendisi Arşimet, M.Ö 287 yılında İtalya’nın Sicilya kentinde Sirakuza’da doğar.
Kral Hiero’nun oğlu Gelon’a adadığı Sandreckoner adlı el yazmasında paylaştığı bilgiye göre, babasının astronom Phidias olduğu söyler. Kimi kaynaklara göre ise soylu bir ailedendir; babası Sirakuza Kralı Hiero’nun arkadaşı veya akrabasıdır. Kesin olmamakla birlikte, 12 yaşında İskenderiye’de tarihin en ünlü üniversitelerden biri Museum’da eğitim görüp, matematikçi Öklid’in öğrencisi olduğu söylenir. Ardından Sicilya’ya döner ve hayatının geri kalanını çeşitli alanlarda araştırma ve deneylere adayarak geçirir. Arşimet’in yapıtlarının çoğu, İskenderiye’de bulunduğu dönemde arkadaşları olan dönemin ünlü matematikçiler Kireneli Eratosthenes ve Samoslu Konon ile yazışma şeklindedir ve kuramsaldır.

Domenico Fetti, Archimedes, 1620
Onun mekanik alanında yapmış olduğu buluşlar arasında, bileşik makaralar, sonsuz vidalar, hidrolik vidalar ve yakan aynalar sayılabilir. Bu teknik buluşlarının dışında kalan bilimsel çalışmalarını iki başlık altında toplamak olanaklıdır: Geometri ve fizik
Arşimet’e dünyadan gelip geçmiş üç büyük matematikçiden (Newton, Gauss) biri gözüyle bakılır. Arşimet’in matematikte kullandığı ispatlar ve problemleri sunuş biçimi son derece çarpıcı ve özgündür. Onun eserlerinde kullandığı biçimin günümüz geometrisinin en yüksek standartlarında olduğu söylenmektedir. Geometriye yapmış olduğu önemli katkılardan birisi, bir kürenin yüzölçümünün 4r² ve hacminin ise 4/3r³ olduğunu kanıtlamasıdır.

Matematiğe olan katkıları, sadece silindir ve küre hakkındaki çalışmaları değil, başlangıcı matematikçi Knidoslu Eudox’a giden, exhaustion yöntemiyle (şekli düzgün olmayan, alanı yada hacmi bilinmeyen bir cismin alan veya hacmini, alanı ya da hacmi bilinen şekillerle doldurarak, o alanı ya da hacmi hesaplama yöntemi) birçok şeklin alanını hesaplamış olmasıdır. Belgeli olarak bu yöntemin ilk olarak kullanıldığı yer Arşimet’in eserleridir. Arşimet, bu yöntem ile bir dairenin içine ve dışına düzgün kenarlı çokgenler çizip, onların alanlarını hesaplayarak, pi sayısının 3 1/7 ile 3 10/71 arasında bir değeri olduğunu hesaplamıştır. O zamana kadar pi sayısının bilinen değerleri, deneysel, ölçme yoluyla elde edilen değerler idi.
Onun sunduğu bilgiler, örneğin pi sayısı, ilk çağ ve ortaçağ boyunca kullanılmış, ancak yapıtlarının uzun yıllar karanlıkta kalması nedeniyle matematiğe katkısı yapıtlarının 8. ya da 9. yüzyılda Arapça’ya çevrilmesine kadar gerçekleşememiştir.
Arşimet’in bir diğer başarısı ise, eğri yüzeylerin alanlarını bulmak için bazı yöntemler geliştirmesidir. Bir parabolün alanını dörtgenleştirilme yöntemiyle hesaplamıştır. Konuyla ilgili olarak tüketme yöntemine başvuran Arşimet, bir parabol kesmesinin alanının, aynı tabana ve yüksekliğe sahip bir üçgenin alanının 4/3’üne eşit olduğunu ispatlamıştır.

Johnny Shumate, Archimedes
Arşimet, fiziğin statik ve hidrostatik konularında da çalışmış ve denge ilkesini ilk defa formüle edebilmiştir. Statik konusunda benimsediği ilkelerin en bilineni eşit kollara asılan eşit ağırlıklar dengede kalır prensibidir. Ünlü “Bana bir dayanak noktası verin, Dünya’yı yerinden oynatayım” sözü bu ilkelerini iyi bir biçimde betimlemektedir.
Arşimet, sıvıların dengesi kanununu da bulmuştur. Söylenene göre, bir gün Kral İkinci Hieron yaptırmış olduğu altın tacın içine kuyumcunun gümüş karıştırdığından kuşkulanmış ve bu sorunun çözümünü Arşimet’e havale etmiş. Bir hayli düşünmüş olmasına rağmen sorunu bir türlü çözemeyen Arşimet, yıkanmak için bir hamama gittiğinde, hamam havuzunun içindeyken ağırlığının azaldığını hissetmiş ve “Buldum, buldum! (Eureka, eureka!)” diyerek hamamdan fırlamış. Onun bulduğu, su içine daldırılan bir cisim, taşırdığı suyun ağırlığı kadar ağırlığından kaybettiği ve taç için verilen altının taşırdığı su ile tacın taşırdığı su mukayese edilerek sorun çözülebileceği idi. Böylece Arşimet, su içerisine daldırılan bir cisim, taşırdığı suyun ağırlığı kadar ağırlığından kaybeder sonucunu çıkarmıştır. Önce tacın ağırlığı kadar gümüş ve altın almış, sonra sırasıyla ağırlıkları eşit olan gümüş, altın ve tacı su dolu bir kaba batırarak taşırdıkları su miktarını belirlemiştir. Taşan su miktarlarını karşılaştırarak sorunu çözmüş ve kralın kuşkusunda haklı olduğunu belirlemiştir. Bu çalışma, özgül ağırlık kavramına ilk özgün yaklaşım olması bakımından değerlidir.
Arşimet’in araştırmalarından önce, tahtanın yüzdüğü ama demirin battığı biliniyordu; ancak bunun nedeni açıklanamıyordu. Arşimet’in bu kanunu doğada tesadüflere yer olmadığını, her zaman aynı koşullarda aynı sonuçlara ulaşılacağını göstermiştir.

Giuseppe Maria Soli, Archimedes
Yaşadığı dönemde Romalılar, Yunanlılar, Kartacalılar sürekli savaş halinde olduğu için, bilimsel buluşlardan daha çok, silah tasarımlarına değer verilir. Ülkesi, Roma’ya karşı Kartaca ile birleşince, icatlarıyla Romalıları nasıl yenebileceklerinin sembolü haline gelir. Onunla ilgili en önemli bilgi Romalıların Sirakuza’yı kuşatmaları esnasında yaptıklarına ilişkindir. Roma generali Marcellus, Sirakuza’yı kuşattığında, Arşimet’in yapmış olduğu silahlar nedeniyle şehri almakta çok zorlanmıştır. Bunların çoğu mekanik düzeneklerdi ve bazı bilimsel kurallardan ilham alınarak tasarlanmıştı. Örneğin, makaralar yardımıyla çok ağır taşları burçlara kadar çıkarılıyor ve mancınıklarla çok uzaklara fırlatılıyordu. Hatta Arşimet’in aynalar kullanmak suretiyle Roma donanmasını yaktığı da rivayet edilir. Ancak bütün bunlara karşın M.Ö. 212 yılında Romalılar Sirakuza’yı zapt ederler. Söylendiğine göre, bu sırada Arşimet toprak üzerine çizdiği bir problemin çözümünü düşünürken, yanına yaklaşan Romalı askere oradan uzaklaşmasını ve kendisini rahat bırakmasını söyler; ancak asker M.Ö 212’de Arşimet’i öldürür.

Benjamin West, Cicero And The Magistrates Discovering The Tomb Of Archimedes, 1797
Vasiyeti üzerine mezar taşına silindir içine sokulmuş bir küre çizilir. Çünkü Arşimet’in en çok gurur duyduğunu söylediği çalışması budur, bir kürenin hacminin, içine tam olarak sığacağı silindirin hacmine oranı. Bu oranı Arşimet üçte iki olarak bulur ve silindirin hacmi bilindiği için kürenin hacmi tam olarak hesaplanmış olur. Arşimet’in mezarı zaman içinde kaybolur. Yaklaşık üç yüz yıl kadar sonra Sicilya’da konsül yardımcılığı sırasında, Cicero üzerinde bir silindir ve küre şekli bulunan, Arşimet’e ait olduğu düşünülen bir mezartaşı bulur. Ancak bugün bu mezartaşı kayıptır.
Bir kürenin hacmini merak eden ilk kişiyi bilmiyoruz, ama bunu hesap etmeye cüret eden ilk kişinin Arşimet olduğunu biliyoruz. Bugün bu hesaplamayı yapmak için integral teknikleri kullanıyoruz. Ancak integral hesap, Arşimet’ten yaklaşık 1900 yıl sonra bulunacaktır. İlginç bir ayrıntı ise Arşimet’in içinde hacim hesabının da bulunduğu Metodlar adlı eserinin yaklaşık iki bin yıl ortadan kaybolduktan sonra, bu yüzyılın başında İstanbul’da ortaya çıkmasıdır.
Fener’de bulunan Ayios Yeorgios Metokhion Kilisesi’ni ilginç kılan mimari özelliklerinden ziyade, Arşimet’in yedi çalışmasının 10. yüzyıl kopyalarından üçünün, Metodlar, Stomachion ve On Floating Bodies’in içerde korumuş olması. Bugüne kadar ulaşabilmeleri bir mucize gibi görünse de işin aslı şu, bu çalışmaların yazıldığı parşömenler, 13. yüzyılda bir dua kitabının yazılmasında yeniden kullanılmışlar. Arşimet Parşömeni de denilen bu çalışmanın İstanbul’da yapıldığı hemen hemen kesin gibi, ancak 1906 yılında Johan Ludvig Heiberg tarafından ortaya çıkarılmış. Bugün ABD Baltimore’daki Walters Sanat Müzesi’nde korunuyorlar.
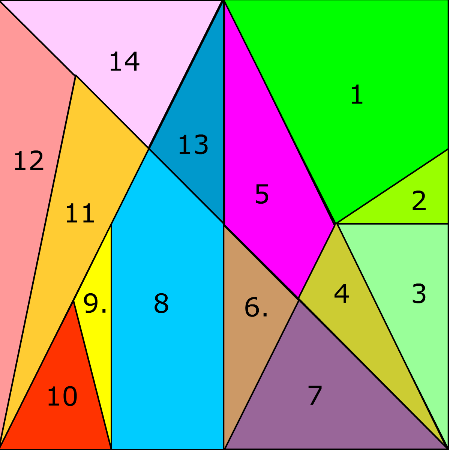
İngilizcede stomachion olarak bilinen bu yapboz, Arşimet tarafından oluşturulduğu düşünüldüğünden Arşimet yapbozu olarak adlandırılmıştır. Yapboz 14 farklı boyuttaki şekilden oluşmaktadır. Oyunun amacı 14 ayrı parçanın bir kare oluşturacak şekilde bir araya getirilmesidir. Klasik metinlerde geçen bu Yunanca kelime, hem bu oyunu hem de karın ağrısını ifade etmek üzere kullanılmakta. Oyun adını karın ağrısına neden olacak kadar zor olmasından almıştır diye düşünebiliriz.
Bu 14 parça kullanılarak kaç farklı şekilde kare oluşturulabilir? Bu soruyu yanıtlamak hiç de kolay değil. Ne yazık ki el yazmalarının son üç yaprağı yüzyıllar önce koparıldığından Arşimet’in bu soruyu nasıl yanıtladığını bilemiyoruz. Çünkü stomachion ile ilgili sadece bir yaprak kalmış. El yazmalarının tamamen gün ışığına çıkarıldığı 2003 yılına kadar Arşimet’in bu oyunu sadece bir yapboz olarak ele aldığı düşünülmüştür. Oysa ki matematikçi Reviel Netz, tam olarak okunamayan o tek yapraktaki bazı ifadelere bakarak, bir oyun olarak ilgilenmenin ötesinde Arşimet’in stomachion’a matematiksel bir yaklaşım getirmiş olabileceğini düşünmektedir.
Kaynak
Arşimet’in Küreleri, Mühendislik Tarihi, Archimedes, Suyun kaldırma Kuvveti ve Gemiler Bağlamında Bilim ve Teknoloji, Arşimet, Matematiğin Kısa Bir Tarihi, Arşimet, Ron Graham, Persi Diaconis ve bir oyun

















