Paradoks, ilk bakışta doğru olan bir ifade veya akıl yürütme etkinliğinin bir çelişki oluşturması, çıkmaza sürüklemesi ve durumun içinden çıkılamaz bir hal almasıdır. Paradoksal bir ifade ya da akıl yürütme kendi içindeki bu çıkmazını, kendi dışında bir açıklamaya yönelmeden ya da ek öncüle ihtiyaç duymadan çözememektedir. Bu nedenle paradoksal önermeler, “ya doğru ya yanlış” olarak ifade edilebilecek bir durumu değil, “ne doğru ne de yanlış” olarak belirlenebilecek mantıksal çelişkiyi, karar verilemez hali ve çözümsüz durumları göstermektedir. Dolayısıyla böylesi bir önermenin ya da akıl yürütmenin paradoksallığı, çıkmazlardan birinin seçimiyle de çözülememektedir. Öyle ki paradoksal ifade; doğru kabul edildiği zaman yanlış, yanlış kabul edildiği zaman da doğru olmakta ve bu nedenle paradokslarda mantıksal manada zorunlu, açık seçik ve kesin bir sonuca ulaşılamamaktadır. Zira farklı bakış açılarına ilişkin olarak paradoksal ifadeye verilen yanıt da farklılık arz etmektedir. O nedenle paradoks, çözülemez bir sorun olarak karşımızda durmaktadır. İşte bu çözümsüzlüğün fark edilmesi, esasında düşüncenin başlangıç noktasının fark edilmesidir.

1. Yalancı Paradoksu
Yalancı Paradoksu Giritli Epimenides’e ve Euclid’in öğrencisi Knossoslu Eubullides’e kadar giden bir yol içinde bulunur. Epimenides’in “ Κρῆτες ἀεί ψεύσται-Bütün Giritliler yalancıdırlar” sözü, “Epimenides Paradoksu”, “Yalancı Paradoksu” veya “Giritli Paradoksu” olarak anılır. Aristoteles’ten sonra yoğun bir şekilde tartışılmış olan bu paradoks, 20. yüzyıla geldiğimizde mantığın temelleri üzerine yapılan incelemelerde önemi yeniden fark edilmiştir. Özellikle Bertrand Russell’ın mantık ve matematik üzerine incelemelerde yalancı paradoksunu yeniden keşfinden sonra Wittgenstein, Tarski ve Kripke gibi modern filozoflar bu paradoksun önemi ve çözümü üzerinde durmuşlardır. Epimenides paradoksu mantıktaki bir sorundur. Problemin bir başka sürüm de Douglas R. Hofstadter’in, Gödel, Escher’in Bach isimli eserinde bulunur.
– Eğer “Bütün Giritliler yalancıdır” önermesini doğru kabul edersek, kendisi de Giritli olan Epimenides’in yalancı olması gerekir. Eğer Epimenides yalancıysa, tüm söyledikleri gibi, “Bütün Giritliler yalancıdır” önermesinin de yanlış olması gerekir. Doğru söylediğine inanırsak yalan söylediğini anlıyoruz. Önermenin hem doğru hem yanlış olduğu sonucu çıkar.
– Eğer “Bütün Giritliler yalancıdır” önermesi yanlış kabul edersek, kendisi de Giritli olan Epimenides’in doğru söylüyor olması gerekir. Şu halde, “Bütün Giritliler yalancıdır” önermesi doğru olmalıdır. Yine çelişkili bir sonuç çıkar.
-Bir önerme hem doğru hem yanlış olamaz.
Modern dönemde ise bu paradoks, “Bu cümle yanlıştır” şeklinde ifade edilmiştir. Eğer bu cümle doğru ise yanlıştır ve yanlış ise doğrudur. Eğer bu cümleyi doğru kabul edersek aslında cümle yanlıştır, yanlış kabul edersek de cümle doğrudur. Önermeyi hem doğru hem de yanlış kabul etmek de mümkün değildir. Paradoksun başladığı nokta da burasıdır.
Burada gözden kaçırılan ve yıllarca matematikçilere yanlış hesaplamalar yaptıran küçük bir püf noktası vardır ve o da şudur: “Bütün Giritliler yalancıdır” önermesinin tersi, “Bütün Giritliler doğrucudur” değildir. doğrusu “En az bir Giritli vardır ki, doğrucudur” olması gerekmektedir. Her kelimesinin tersinin en az bir cümlesi olduğunun keşfinden sonra matematikteki bu tıkanıklık aşılmış, ve aslında Epimenides paradoksunun ortadan kalktığı söylenebilir. Bu bilgi ışığında değerlendirdiğimizde, “Bütün Giritliler Yalancıdır” önermesi yanlışsa, “En az bir Giritli doğru söyler” önermesi doğrudur. Bunlardan birinin Epimenides olması mümkün olduğundan, paradoksu çürütür.

Ferraresisch, Theseus und Ariadne, 1540
2. Theseus’un Gemisi Paradoksu
Theseus’un Gemisi Paradoksu, Yunan mitolojisinde bahsi geçen mitolojik bir olayın, işletme litaratürüne paradoks olarak aktarılmış halidir. Theseus, Dor ırkının yüce savaşçısı Herakles’in örneklendirmesi üzerine Atina’da söylentilerle doğmuş bir kişidir; efsanesi ise Herakles efsanesinin nakışları ile bir araya getirilmiş, bu kuramlara Atina’nın ilkelerini yansıtan bireysel ve toplumsal birkaç tema eklenmiştir. Atinalılar Theseus’u destansı değil de tarihi birey olarak sayarlardı. Theseus, Atina’nın tüm eskiçağ savaşçıları içinde kendisine en çok saygı edilen savaşçılardandır ve hepsi içinde en popüler olanıydı.
Theseus’un, yıllar geçtikçe yıpranan ve yıpranan kısımlarını sürekli olarak onardığı bir gemisi vardı. Theseus’un Gemisi yıllar geçtikçe geminin tahtaları çürüdükçe yeni parçalar ile değiştirilir. Ne var ki, bir gün geminin herhangi bir yerinde değişmeyen parçası kalmaz olur. Bu durumda gemi hala Theseus’un Gemisi olarak kabul edilir mi, yoksa artık o başka bir kişiye ait gemi haline mi gelmiştir? Theseus’un Gemisi Paradoksu maddesel ve felsefi açıdan Heraklitos, Aristotales gibi filozoflar tarafından tartışma konusu olmuştur. Theseus’un Gemisi, filozofları eski çağdan bu yana uğraştıran bir konudur.
Aristotales; bir objenin netliğini şekilsel sebep tanımlar, buna bağlı olarak Theseus’un gemisi, her zaman gemi olarak kalmış ve değişmemiştir, aksi halde şekli değişmemiştir. Aristo’nun öbür bir nedeni sonuncu neden yahut maksattır. Theseus’un gemisinin parçaları değişim gösterse de, maksadı (Theseus’u taşımak) değişmemiştir, hâlen o gemidir. Sonuncu olarak etkin sebep bir şeyin kimin muhatabı ve nasıl yapıldığıyla ilgilidir. Theseus’un gemisini ilk inşa eden ustalar ve onların aletleri, gemiyi tamirlerle bire bir aynı olduğu için, bu sebeple gemi değişmemiştir.
Heraklitos’a göre ise nesneler sürekli değişebilir. Bu sebeple yukarıdaki tartışılan tez bir paradoks kabul edilmez, Theseus’un gemisi, Atina’ya adım attığı günün ertesinde, Theseus’a ait bir gemi olmaktan çok başka bir gemi olmuştur.
Bu paradoks sınırları birbirinden ayırmak konusunda bir soru ortaya koymaktadır. Aslında Theseus’un gemisi ne zaman aynı gemi olmaktan çıkmıştır? Genelde insanlar daha çok, kolay fark edilen değişimlerle ilgililerdir.

3. Russell Paradoksu
Çok bilinen Yamyam Paradoksu’na göre Yamyamlar bir mantıkçı yakalarlar, mantıkçıya:
– Biz her yakaladığımız yabancıyı yeriz. Kimini haşlayıp, kimini kızartıp yeriz. Avımıza bir soru sorarız. Avımız soruyu doğru yanıtlarsa haşlarız, yanlış yanıtlarsa kızartırız.
Yamyamlar mantıkçıya şu soruyu sorarlar:
– Seni haşlayıp da mı yiyeceğiz, yoksa kızartıp da mı yiyeceğiz? Mantıkçı şöyle yanıtlar:
– Kızartacaksınız!
Bu soru ve yanıtla, mantıkçı ne haşlanır, ne de kızartılır. Bir an, mantıkçının kızartılacağını varsayalım. O zaman mantıkçının yanıtı doğru olur. Ama yanıt doğru olduğundan, yamyamların kendi kurallarına göre mantıkçının haşlanması gerekmektedir. Demek mantıkçı kızartılamaz. Şimdi de mantıkçının haşlanacağını varsayalım. O zaman mantıkçının yanıtı yanlış olacak. Yanıt yanlış olduğundan da kızartılması gerekmektedir. Demek mantıkçı haşlanamaz. Yamyamlar tam bir kısır döngüye girerler. Kızartsalar haşlamaları gerekecek, haşlasalar kızartmaları. Sonuç olarak mantıkçı kurtulur.
Yukarda sözünü ettiğimiz paradoksun bir benzerini ünlü matematikçi ve filozof Bertrand Russell 1901’de, daha henüz 28 yaşındayken bulur. O günün matematiğinin çelişkiden yoksun olmadığını gösteren bu paradoks tahmin edileceği gibi matematikçileri sarsmış ve onları matematiğin temelleri üzerine daha derin düşünmeye zorlamıştır . Russell paradoksunu sembollerle ifade etmek gerekirse ;
R={x∣x∉R} şeklinde tanımlayabiliriz. Sözel olarak ifade etmek gerekirse; bu kümenin elemanı, aslında bu kümenin elemanı değildir. x, R’nin elemanı olsaydı; R’nin elemanı olmayacaktı. Buna göre R kümesi kendini kapsar mı ? sorusu üzerinde düşünebiliriz. R, R’nin elemanı olsaydı, R’nin elemanı olmayacaktı. İlk bakışta kendini barındırmıyor diyebiliriz. Ancak tanımdan yola çıkarsak R, R’nin elemanı değilse, R’nin elemanıdır. Yani kendini barındırır. Hem kendini barındırıp hem de barındırmama durumu bir paradoks oluşturur ve bu paradoks Russell Paradoksu’dur.
Russell paradoksu şöyle açıklanabilir. “Kendi kendisinin üyesi olmayan tüm kümelerin kümesi, kendisinin bir üyesi midir?” Eğer üyesidir dersek, tüm kümelerin kümesinin bu kümede işi ne? Çünkü bu küme sadece kendisinin üyesi olmayan kümelerin kümesidir. Eğer üyesi değildir diyorsak, bu kez de tüm kümelerin kümesi kendine üye olmayan bir küme olur, o zaman da tüm kümelerin kümesini bu kümeye dâhil etmemiz gerekir ama bu durumda da bu küme kendine üye olabilen bir küme olur. Yani ortaya bir kısır bir döngü çıkar.

Bu paradoksun da katkısıyla, son yıllarda ortaya çıkan puslu mantığa göre, bütün önermeler doğru ya da yanlış olarak kategorize edilemez. Bu da akıllara şu soruyu getirir; matematikte çelişki var mıdır ?
Uzun yıllar boyunca tartışma konusu olan bu soruya, 1930 yılında Kurt Gödel bir açıklık getirmiştir. Matematikte çelişkinin olmadığının kanıtlanamayacağını ispatlamıştır. Ancak bu matematiğin çelişkili olmadığı anlamına değil, bunun kanıtlanamayacağı anlamına gelir. 1901 yılında ortaya atılan Russell Paradoksu, Kurt Gödel’in bu büyük ispatının önünü açmıştır da diyebiliriz. Çünkü Russell Paradoksu’nda matematiğin çelişkisiz olmadığı gösterilmiş, matematik dünyasındaki en büyük tabulardan birini sarsmıştır.
Modern mantığın kurucularından biri olan ünlü Alman matematikçi ve mantıkçı Frege; 1893’te yayınladığı Aritmetiğin Temelleri adlı ünlü çalışmasında aritmetiği sağlam şekilde inşa edilmiş bir kümeler kuralına indirgemek istemiştir. 1902’de kitabın tam ikinci cildini baskıya verdikten sonra, Russell’dan aldığı mektupla adeta yıkılmış, yıllarca emek verdiği çalışması ve teorisi bir mektupla çürümüş ve yok olmuştur, kendisi de bu olayı şöyle anlatmıştır:
“Bir bilim insanı için, yapıtı biter bitmez temellerinin yıkılmasından daha korkunç bir şey düşünülemez. Yapıt tam baskıya hazırlanırken Bay Bertrand Russell’dan aldığım bir mektup beni işte bu duruma soktu.”
Sanılanın tersine matematikte küme kavramı, bu yüzyılda ortaya çıkmamıştır. Bu kavram, açıkça adı söylenmese de, Yunanlılardan beri biliniyordu. Daha sonra Alman Matematikçi Georg Cantor, küme kuramını bilimsel olarak ortaya attı. O zamanlar bir nesnenin küme olabilmesi için bir takım koşulların gerektiği bilinmiyordu. Akla gelebilecek tüm nesnelerin bir küme oluşturabileceği sanılıyordu. Hele küme gibi doğal bir kavramın günün birinde matematiği çelişkiye düşüreceği akıllara hiç gelmiyordu. 19. yüzyılın sonuna dek, matematikçiler gördükleri, düşünebildikleri her matematiksel nesne topluluğuna küme adını vermekten çekinmediler. Tam sayılar kümesi, çift sayılar kümesi, bir düzlemin noktaları kümesi, bir düzlemin eğrileri kümesi, bir düzleme çizilebilen dikdörtgenler kümesi, bu kümelerin bileşimi, bir kümenin altkümeleri kümesi. Her topluluk bir küme oluşturabilirdi. Hatta tüm kümeler kümesi bile… Küme kavramı o zamanların matematikçileri için sezgisel bir kavramdı. Yıllar boyunca matematikçiler bir kümenin oluşması için kısıtlayıcı koşullara gerek görmediler.
Bertrand Russell, paradoksunu ortadan kaldırmak amacıyla, 1908’de tipler kuramı adı verilen bir kuram ortaya atar. Tipler kuramı kümeleri derecelendirir. Örneğin, dördüncü dereceden bir kümeyi tanımlamak için ancak birinci, ikinci ve üçüncü dereceden kümeler kullanılabilir. Böylece A adını verdiğimiz, “tüm kümeler kümesi” diye bir küme matematikte yasaklanmış olur ve Russell’ın paradoksu, paradoks olmaktan çıkar. Yani Russell akla gelen her nesnenin küme olmasını yasaklayarak, matematiği değiştirmiş, çelişkisiz bir matematik yaratmıştır. Ünlü Fransız matematikçisi Poincaré’nin de dediği gibi, kurtlardan korumak için sürünün çevresine bir çit çekilmiştir.
Bilim dünyasında yüzyıllarca doğru bilinen bir teori ertesi gün çürütülebilir; yerine yenisi, daha iyisi, daha geniş kapsamlısı da gelebilir.

4. Alf Ross Paradoksu
Alf Niels Christian Ross, bir Danimarkalı hukuk ve ahlaki filozof ve uluslararası hukuk bilginiydi. En iyi İskandinav hukuk gerçekçiliğinin lider üslerinden biri olarak bilinir. Ross’un paradoksu diye bilinen Alf Ross Paradoksu, yukarıda anlattığımız Yalancı Paradoksu ile yakın akrabadır. Felsefi veya mantıksal paradokslara verilebilecek en iyi örneklerden biri Yalancı Paradoksu’dur. Bu paradoksta, “Bu cümle yanlıştır” ifadesi şaşırtıcıdır; çünkü eğer cümle yanlışsa doğru, doğruysa yanlış olmaktadır. Bu tür cümleler rasyonel çözümlemelere direnen ifadelerdir.
Alf Ross’a göre kendine atıfta bulunan normlar anlamsızdır; bunun nedeni kendine atıfta bulunan cümlelerin anlamsız olmasıdır. Bazı hukuk kuralları başka hukuk kurallarının nasıl değiştirileceğini düzenler. Ama bu değiştirmeyle ilgili kurallar da çoğunlukla daha üstte yer alan ve bu kuralların nasıl değiştirileceğini düzenleyen kurallar tarafından değiştirilebilir. Anayasa değişikliğini düzenleyen kural gibi, değişikliği düzenleyen kural, kendi sistemi içinde en üstte yer alıyorsa, bu kural sadece bu kuralın getirdiği usule uyularak değiştirilebilecektir.
Alf Ross paradoksu anayasada, anayasa değişikliğini düzenleyen hükmün kendisi, bu hükmün değiştirilmesinde kullanıldığında ortayla çıkmaktadır. Ross’a göre anayasa değişikliğini düzenleyen hükmün kendisinin değiştirilmesi kavramsal ve mantıksal güçlüklerle dolu olduğundan, bu paradoksun çözümü için değiştirilemeyen ve yazılı olmayan temel bir normun varlığının varsayılması gerekmektedir.
Ross, paradoksu şöyle örnekler: Anne–baba otoritesinin temel normunun şöyle olduğunu düşünelim: Çocuklar (S) her açıdan mutlak bir biçimde babalarının (F’nin) iradesine uymak zorundadır. Eğer F, S’ye benim emirlerime artık uyma derse, bu serbest bırakma bu temel normdan kaynaklanamaz; çünkü sonuç (serbest bırakma) ilk öncülle (ebeveyn otoritesiyle ilgili temel normla) çelişmektedir. Bir başka deyişle eğer S, babası F böyle söylediği için babasının emirlerinden bağımsız olarak hareket edecek olsa dahi hâlâ ebeveyn otoritesini kabul etmektedir ve gerçek anlamda özgür olamamıştır. Çünkü babasının vereceği yeni bir emirle bu özgürlüğü sonlanabilir. Benzer bir biçimde bir ülkede temel normun meclisteki milletvekillerinin yüzde 60’nın oylarıyla anayasanın değiştirebileceğini kurallaştırdığını varsayalım. Eğer bu çoğunluk gelecekte anayasa değişikliği için milletvekillerinin yüzde 70’nin çoğunluğunun oyunun gerekli olduğuna karar verecek olursa, bu yeni temel norm eskisinden kaynaklanamaz.

5. İkizler Paradoksu
İkizler paradoksunu anlamak için öncelikle Einstein’ın 1911 yılında yazdığı şu satırlara göz atalım:
“Bir kutunun içine canlı bir organizma yerleştirmişsek. Öyle bir ayarlama yapılabilir ki, keyfi derecede uzun bir yolculuktan sonra organizma neredeyse hiç değişmemiş bir şekilde başlangıç yerine geri dönebilir. Ancak bu sırada başlangıç noktasında duran organizmalardan yeni nesiller üremiş olacaktır. Eğer yolculuk neredeyse ışık hızıyla yapılmışsa, hareket eden organizma için tüm yolculuk çok kısa sürecektir.”
Dolayısıyla ikiz kardeşlerden biri yolculuk yapıyor, diğeri durağansa; zaman yolculuk yapan kardeş için daha yavaş akacak ve geri döndüğünde kardeşini kendisinden çok daha fazla yaşlanmış bulacaktır. Einstein, bu durumu bir paradoks olarak değil özel görelilik kuramının doğal bir sonucu olarak görmüştü. Bu düşünce deneyinin başkaları tarafından paradoks olarak görülmesinin nedeniyse: Birinci kardeşin bakış açısına göre ikinci kardeş belirli bir anda kendisinden uzaklaşmaya başlamış ve uzun bir yolculuk yaptıktan sonra geri gelmiştir. Ancak aynı fiziksel olaya ikinci kardeş açısından bakarak da benzer sözler söyleyebilirdik. İkinci kardeşin yolculuğu sırasında birinci kardeş önce ikinci kardeşten uzaklaşmakta daha sonraysa yaklaşmaktadır, yani ikinci kardeşe göre hareket etmektedir. Peki öyleyse, neden ikinci kardeş daha genç kalır?
Durağan olan kardeş daha çok yaşlanmıştır, çünkü iki uzay zaman noktası arasında eylemsiz hareket etmiştir. Uzaydaki bir noktadan harekete başlayıp tekrar aynı noktaya dönen bir gözlemcininse eylemsiz hareket etmesi imkânsızdır. Dolayısıyla yolculuk yapan kardeş iki olay arasındaki zaman farkını daha az ölçecek, yani daha az yaşlanacaktır.
1911’de Paul Langevin ile başlayarak, bu paradoksun çeşitli açıklamaları olmuştur. Max von Laue, 1913’te, seyahat eden ikizin iki ayrı atalet çerçevesinde olması gerektiğini (biri çıkışta, diğeri geri dönüşte) ve bu çerçeve değiştirmenin yaşlanma farkının nedeni olduğunu savundu. Albert Einstein ve Max Born tarafından ortaya konan açıklamalar, yaşlanmayı ivmenin doğrudan bir etkisi olarak açıklamak için Gravitasyonal (kütlesel çekim kuvveti) zaman genişlemesini öne sürdü. Einstein’ın 1905 yılında ileri sürdüğü özel göreliliğin iki postülasının; ilki, birbirlerine göre düzgün doğru hareket yapan tüm gözlemciler için ışık hızı aynıdır. İkincisi ise birbirlerine doğru hareket halindeki tüm gözlemciler için fizik kanunları aynıdır. Yanı sıra evrendeki bilinen 3 boyut haricinde birde zaman boyutunun olduğunu ortaya koyması fizik dalındaki en büyük devrim olarak nitelendirilmektedir.

Şimdi zamanın göreceliği kavramını en iyi şekilde özetleyen ve çok popüler bir örnek olmasına rağmen hala kavram hatalarının yapıldığı ikizler paradoksuna astrofizik bilimleri profesörü Richard Gott’un özgün anlatımıyla bakalım: “İkiz kız kardeşler, Dünya ve Evren bu paradoksun klasik örneğidir. Tahmin ettiğiniz gibi Dünya Dünya’da kalır, Evren ise bir roketle ışık hızının %80 hızıyla Alpha Centauri yıldızına gider. Alpha Centauri Dünya’dan 4 ışık yılı uzaklıkta olduğuna göre, Evren’in oraya varışı 5 ışık yılı sürer. Evren’in saati Dünya’nın saatine göre %40 daha yavaş ilerler, Bu nedenle Evren bu yolculukta sadece 3 yıl yaşlanırken; Dünya, Evren’in yıldıza varışını 5 yıl olarak ölçer. Evren, Alpha Centauri’ye ulaştığı anda yön değiştirir ve yine ışık hızının %80’i bir hızla geri döner. Dönüş yolculuğu yine aynı şekilde Dünya tarafından 5 yıl, Evren tarafından da 3 yıl olarak ölçülür. Sonuç olarak Evren Dünya’ya vardığında; kendisinin toplam 6 yıl, Dünyanın ise toplam 10 yıl yaşlandığını görür. Yani Evren dünya zamanına göre 4 yıl ileri gitmiştir. İşte paradoks tam bu noktada ortaya çıkar.
Evren ışık hızının %80’i hızla Alpha Centauri’ye doğru giderken, roketin camından bakıp, aslında Dünya’nın ışık hızının %80 hızıyla gittiğini ve kendisinin sabit durduğunu ileri sürebilir. Bu düşüncedeki yanlış şudur; İkiz kardeşler aynı deneyimleri yaşamadılar. Dünya’da bulunan Dünya, yön değiştirmeksizin sabit bir hızla hareket eden bir gözlemci, Dünya’nın Güneş etrafındaki hızı ihmal ediliyor olduğundan Einstein’ın ilk postülasını sağlar. Buna karşın Evren, yön değiştirmeksizin sabit hızla hareket eden bir gözlemci değildir. Evren, Alpha Centauri’ye vardığında yön değiştirir. İşte üzerinde durulması gereken en kritik nokta “yön değiştirme” olgusudur. Şimdi Evren’in bu yolculuk sırasında neler düşündüğüne bakalım: Evren, Alpha Centauri’ye doğru giderken camdan bakar ve Dünya’nın ışık hızının %80 i hızla hareket ettiğini görür. Alpha Centauriye vardığında saatine bakar ve 3 yıl geçtiğini görür, bunun üzerine ışık hızının %80’i hızla hareket eden Dünya’daki Dünya’nın kaç yıl yaşlandığını bulmak için işlem yapar ve çıkardığı sonuç 1,8 yıl olur. Yani kendisi 3 yıl, Dünya ise 1,8 yıl yaşlanmıştır Evrene göre. Alpha Centauriye vardığında Evren konumunu Dünyaya doğru çevirir. İşte tam bu yön değiştirme hareketini yaptığı anda uzay-zamanı farklı bir eğimle diler ve aslında hareket edenin kendisi olduğunu algılar. Dönüş yolu boyunca yine ışık hızının %80’i hızla hareket eden ve Dünya’ya varan Evren, yaptığı hesaplar sonucunda dönüş yolu boyunca Dünya’nın 8,2 yıl dolayısıyla 8,2(dönüş) +1,8(gidiş) olmak üzere toplamda 10 yıl yaşlandığını kendisinin ise 3+3 yıl olmak üzere 6 yıl yaşlandığı sonucuna varır. Görüldüğü gibi ikizler paradoksu, mantıksal çelişki anlamında bir paradoks değildir. Evren’in Dünya’daki olayların eş zamanlı olduğuna dair olan fikri dönüş hareketi sonrasında tamamen değişir ve aslında hareket edenin kendisi olduğunu algılar. Yani böylece her iki kardeşinde yaşları hakkındaki hesaplarının doğru olduğu ortaya çıkar.
Burada da çok net bir biçimde görüldüğü üzere zaman göreceli bir kavramdır. Ama bu görelilik fizik yasalarını kesinlikle etkilememektedir. Fizik yasaları sahip oldukları simetri sayesinde her koşulda kesinliğini muhafaza etmektedir. Şu unutulmamalıdır ki, eğer hız, zaman gibi kavramlardan bahsediyorsak anlam kargaşasını önlemek için mutlaka bir referans noktası belirtmeliyiz. Kim bilir beklide zaman kavramını daha ayrıntılı bir şekilde anlayabilirsek birçok bilim adamının ve bilim-kurgu yapımcısının fantezisi olan geleceğe ve geçmişe yolculuk rutin yapılan işlerden birisi olacaktır.
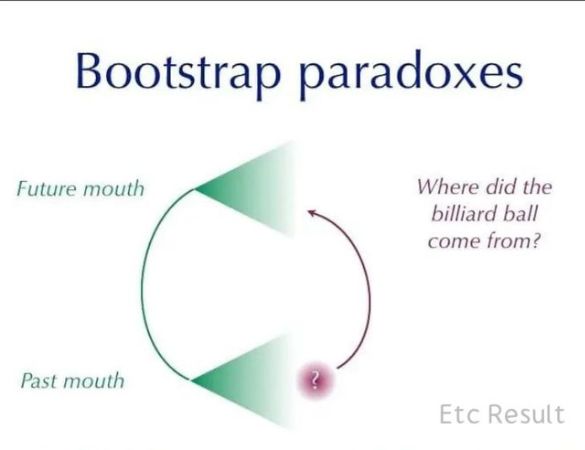
6. Bootstrap Paradoksu
Birçok film ve diziye konu olmuş Bootstrap Paradoksu ya da Türkçesiyle Ayakkabı Bağı Paradoksu. Paradoksun konusu, çoğu paradoksta olduğu gibi zaman yolculuklarına dayanır. Temel fikir ise şu yönde; kimse kendi kendisini, kendi ayakkabısının bağcığından tutarak havaya kaldıramaz. Buradaki imkânsızlığın zaman ile ilişkisi ise çok daha ilgi çekici. Bu paradoksa göre eğer geçmişe doğru bir yolculuk mümkün olabilirse, zaman içerisindeki bilgi ve ürünler, hiç icat edilmeden de var olabilir.
Anlaşılması zor olabilir; bir örnekle açıklayalım. Bir gün evinizde zaman makinesini icat etmek için çalışıyor ancak bir türlü başarılı olamıyorsunuz. Kahvenizi içerken bir anda yanınızda birisi beliriyor; bu kişi sizin gelecekteki halinizden başkası değil! Size fazla kahvenin zararlı olduğundan bahsettikten ve elinizdeki kahveyi alıp, zaten zaman makinesini icat ettiğinizi, vakit kaybetmemeniz için taslakları yanında getirdiğini söyledikten sonra yok oluyor. Siz o taslakları kullanarak zaman makinesini icat ediyorsunuz ve geçmişe giderek genç halinize o makinenin taslaklarını veriyorsunuz. Peki, bu durumda zaman makinesini ilk icat eden kim? O taslaklar olmasaydı, belki de makineyi asla icat edemeyecektiniz, peki bu durumda gelecekteki haliniz o taslaklara nereden ulaştı?
Bir başka bilinen örnek ise Einstein ile ilgili. Bu hikâyeye göre Einstein evinde otururken bir adam gelir ve Einstein’a “Görelilik Teorisi’ni bulan sensin. Normalde teoriyi bulduğun yıla gidecektim ama yanlışlıkla bu yıla denk geldim.” der ve henüz Görelilik Teorisi’ni bulamamış Einstein’a, yazdığı makaleyi verir. Einstein bu makaleyi aynı şekilde yayımlar ancak içi hiçbir zaman rahat etmez çünkü makaleyi yazan kendisi değildir, o makale ona verilmiştir. Bu paradoksa göre eğer geçmişe doğru bir yolculuk mümkün olabilirse, zaman içerisindeki bilgi ve ürünler, hiç icat edilmeden de var olabilir.
Peki, o adam neden makaleyi Einstein’ın yazdığını söylemiştir? Bu makaleyi ilk yazan kimdir? Bu kısır döngüden kurtulmanın iki farklı yolu var. İlki, zamanda yolculuğun asla mümkün olamayacağı kanısını benimseyip bu paradoksu umursamamak. İkincisi ise, konuyu daha da derinleştiren seçenek, paralel evrenler teorisi. Bu teoriye göre geçmişe döndüğünüzde aslında kendi gerçekliğiniz ve zaman çizginize değil, bir başka gerçekliğe ve zaman çizgisine gidiyorsunuz. O farklı gerçeklikteki siz zaman makinesini belki de asla bulamayacaktı ancak siz kendi gerçekliğinizde bu makineyi buldunuz ve alternatif bir evrende de geleceği şekillendiriyorsunuz. Ancak bu yola paradoksu çözmek yerine ondan kaçmış oluyorsunuz. Ayakkabı Bağı Paradoksu tek bir zaman çizgisi ve tek bir gerçeklikten bahsediyor, milyonlarca alternatif gerçeklik ve birbirinden farklı milyonlarca zaman çizgisi bu konuya dâhil değil. Ve bu durumda yine başladığımız yere dönüyoruz.
Zaman yanılgılarının en net örneklerinden olan bu paradoks, geçen zamana karşın hâlâ algıları yerle bir etmeye devam ediyor. Gün olur da zamanda ileri geri gitmek mümkün olursa bu gibi durumlar elbette ki yaşanacaktır. Fakat şu anda böyle bir çalışma görünmüyor.

Jan Cossiers, Prometheus Carrying Fire
7. Prometheus Paradoksu:
Yunan Mitolojisi’nde Prometheus, insanlardan bilgi ateşini çalan Zeus’tan bilgi ateşini tekrar çalarak insanlığa geri vermiştir. Bu nedenle mitolojide Prometheus’tan bahsedilirken, zekâsı ve kurnazlığı ile ünlü olduğundan, hatta Tanrılara karşı insanlığın yararına çalışan bir kahraman olduğundan bahsedilir.
Tanrılar ve ölümlü olanlar Mekone’de toplandılar. Ölümlüler tarafından adak edilen her kurban tanrılara pay edilerek gönderiliyordu. Bu arada tanrıları sevmeyen, insanların hâkimiyet kurmasını isteyen Prometheus, insanların karşısında Zeus’u küçük düşürmenin planlarını yapar. Zeus adağın iyi olmayan yanı seçerse, aslan payı ölümlülerde kalacaktı; aksi olursa, hâkimiyet yine tanrıda kalacaktı. Bu yüzden Prometheus, kurban olarak sunulmuş bir öküzü keserek ikiye parçalar, bir tarafa etini koyar, üzerine işkembeyle kapatır; diğer tarafa ise kemikleri koyar, üzerine parlak yağla ile kapatır. Prometheus, Zeus’a parçalar arasında birini seçmesini söyler ve Zeus da yağ ile kaplı olan payı seçer. Prometheus tarafından kandırıldığını ve kemik yığınını seçtiğini fark eden Zeus öfkelenip ve insanlığı cezalandırmak için insanlardan ateşi alır. Prometheus, Olympos’a çıkar, bir kamışın içine gizlediği kıvılcımı kaçırarak, yeryüzüne insanlığa geri getirir. İnsanoğlu, Prometheus sayesinde ateşe yeniden kavuşur ama Zeus’un öfkesi çok daha fazla artar. Bu nedenle Zeus, Prometheus’u cezalandırmak ister. Prometheus zincirlenerek kayalara bağlanır ve bir kartal, her gece Prometheus’un karaciğerini yemek için tanrılar tarafından görevlendirilir. Kartal gece karaciğerini yer, ancak gün içinde Prometheus’un karaciğeri iyileşir; eziyet böyle devam eder.
Prometheus Paradoksu, toplumsal menfaatleri kendi menfaatlerinden önde tutarak, güç sahibi olan kişilerin yaptıkları haksızlıklar karşısında sessiz kalmama, gerektiği şekilde mücadele etme gibi davranışların bütünü olarak tanımlanabilir.
Prometheus Paradoksu’nun Ana Teması “İdeallerin ve insanların yararına olan unsurların kişisel menfaatlerden daha ön planda olması gerektiği ile ilgilidir“. Ayrıca toplumun çıkarlarını tehdit eden ve gücü elinde bulunduran kim olursa olsun yanlış davranışlar karşısında herkesin mücadele etmesi gerektiği olgusu üzerine yoğunlaşılmaktadır. Son olarak ideallerin gerçekleştirilmesi ve mücadele sırasında akıl unsurunun da ön planda olması gerektiği söylenebilir. Prometheus’ta, yıllarca ceza çekecek olmasına rağmen yapılan haksızlıklar karşısında sessiz kalmamıştır. Ayrıca gücü elinde bulunduranların görevlerini kötüye kullanma davranışı karşısında da sessiz kalmamış ve idealleri uğruna onlarla mücadele etmiştir. Mücadelesi sırasında ise sadece kendi aklına ve inançlarına güvenmiştir.
Prometheus Paradoksu esasında işletme literatüründe yer alan Whistleblowing kavramı ile benzer bir olgu olarak düşünülebilir. Whistleblowing, bir organizasyonda bulunan yasa-dışı ve ahlaki değerlere aykırı olan davranış ve hareketlerin organizasyon içerisinde ve/veya organizasyon dışında farklı bireylere veya kurumlara olumsuzluk yaratmaması için enformasyon sahibi bireyler tarafınca sorunlara odaklanıp çözüm yetkisi ve güce sahip iç ve dış hakimiyete bildirilmesi olarak açıklanır. İşletme hayatında gücü elinde bulunduran yönetici veya kişiler, sahip oldukları yetkileri kullanırken kişisel düşünce ve duygularını alacakları kararlara yansıtmamaları gerekir. Bu nedenle yöneticilerin alacakları kararlar üzerinde sadece akli mental yeteneklerini kullanmaları gerekir.
Kaynak
İslam Düşüncesinde Yalancı Paradoksu ve Hocazade Bursevî’nin Hallu Mağlatati’l-Müsemmâti Bi’l-Cezri’l-Esamm Adlı Risalesi, Mitolojiden Yönetim Literatürüne Yeni Metafor Önerileri, Anayasa Hukukunda “Yalanc›” Alf Ross Paradoksu, Bir Mantık Problemi Olarak Paradoks, Kardinalite, Rusell Paradoksu, Bertrand Russell’›n Paradoksu- Nesin Köyü, Anayasa Hukukunda “Yalanc›” Alf Ross Paradoksu The Liar in Constitutional Law: Alf Ros’s Paradox, İkizler Paradoksu-Bilimgenç, İkizler Paradoksu (twin paradox)- Prof Dr Bilsen Beşergil, Catch Tech- Sayı 5

















